Snipes
From Sudoku Theory
This page is for collecting "nerd snipes" - various tasks to answer questions about minimums, maximums, and counts for all things sudoku.
Classic Sudoku
- The fewest given digits in a classic sudoku is 17; this was proven by McGuire et al. There exist 16 given sudoku with as few as 2 solutions. There are exactly 49158 essentially different 17 given puzzles; the last was found in 2019 (link), and an exhaustive search (link) has confirmed that this is a complete list. List of all essentially different 17 given puzzles.
- For 8x8 (standard, with 4x2 regions), the minimum is 14 givens, proven by Lass, Christoph. (2012).
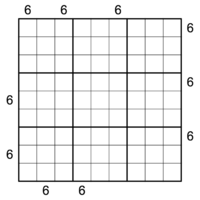
- For 6x6 (standard, with 3x2 regions), the minimum is 8 givens (link), and can even be done symmetrically (link, jovial). The fewest known solutions for 7 givens is 6, by Qinlux (link).
- For 5x5 the minimum is 6 givens, and for 7x7 the minimum is 12 givens. Qiu Yangzhe demonstrated a pattern on latin squares that can be extended indefinitely to find minimums for any prime-sized sudoku (link). The pattern has been theorized to be minimal for all such grid sizes, although not proven for any greater than 8.
- For 16x16 the minimum is 55 givens (link). It is unknown if this can be improved.
- For 10x10 (standard, with 5x2 regions), the minimum is 22 givens (link), found by ton. It is unknown if this can be improved.
- For 12x12 (with 6x2 regions), the minimum is 32 givens (link), found by ton. It is unknown if this can be improved.
- For 12x12 (with 4x3 regions), the minimum is 30 givens (link), found by ton. It is unknown if this can be improved.
- For 15x15 (with 5x3 regions), the minimum is 48 givens (link), found by ton. It is unknown if this can be improved.
- For 20x20 (with 5x4 regions), the minimum is 88 givens (link), found by ton. It is unknown if this can be improved.
- For 25x25 the minimum is 151 givens Template:Citation needed. It is unknown if this can be improved.
- Every solution grid has at least one minimal puzzle with fewer than 22 givens, as shown by Mathemagics and blue. There are exactly four grids which do not have a minimal puzzle with fewer than 21 givens (link).
- The most givens for a minimal classic sudoku is 40. Two examples are known, both found by dobrichev. In the work to find these Sudokus, other high-clue puzzles were catalogued, including more than 6,500,000,000 minimal puzzles with 36 clues. About 2600 minimal Sudokus with 39 clues were also found[1]. This is believed to be the maximum, but it is not proven to be. If dropping the requirement for the uniqueness of the solution, 41-clue minimal pseudo-puzzles are known to exist, but they can be completed to more than one solution grid. Removal of any clue increases the number of the completions and from this perspective none of the 41 clues is redundant. With slightly more than half the grid filled with givens (41 of 81 cells), the uniqueness of the solution constraint still dominates over the minimality constraint.
- The most empty houses in a classic sudoku is 9 (3 boxes, 3 rows, 3 columns). This is the maximum, shown by exhaustive search Template:Citation needed.
- For a 6x6 grid, the most empty houses is 6 (link), found by randomra.
- The most empty diagonals in a classic sudoku is 24 (link) as found by PN.
- The largest rectangle of empty cells in a classic sudoku is 32 cells (4x8). This is believed to be the maximum, but it is not proven to be. If the rectangle is allowed to rotate, then an area of 36 is possible, covering 54 cells and enclosing 27 (link).
- The largest number of consecutive blanks in a classic sudoku string is 34 (link). This is the theoretical maximum.
- The smallest pattern of cells that ensure one or fewer solutions when filled is 48, as shown by trivial171 (link).
- It is possible to have classic sudoku where the given digits do not touch, not even diagonally (link), as shown by jovi_al.
- For an incomplete puzzle, the maximum number of candidate digits that can be placed in a single cell to create a unique solution is 9 (all of them), as shown by Mauricio (link). TopAutism demonstrated that it is possible for such a puzzle to have rotational symmetry (link). The same can be done for 5x5 without symmetry, as shown by Andrewsarchus (link).
Variants
Unless otherwise noted, the minimums for variants are given either for the fewest givens needed for a unique solution (for a global variant), the fewest of a constraint needed for a unique solution with no given digits, or the fewest cells covered by a constraint needed for a unique solution with no given digits.
Global Variants
Irregular Sudoku
- The fewest givens with irregular regions is 8 (link). This is the theoretical minimum, as at least this many digits are needed to disambiguate the digit permutation. It is unknown who first discovered this pattern of regions, but related patterns exist at least as early as 2001 (link). Similar solution grids with a cyclic pattern in the rows and/or columns are useful for many minimal sudoku tasks.
- The fewest Kropki dots with irregular regions (using the same cyclic pattern) is 6, found by rubenscube (link), this is proven to be the minimum.
- The minimum number of regions required for a latin square to be unsolveable is 2, as found by Eric Fox (link).
- There exist irregular sudoku for all grid sizes greater than 3 that have 0 solutions, as proven by Johan de Ruiter (link).
Anti-Knight
- The fewest givens in an Anti-Knight sudoku is 8; there are 4 essentially different puzzles, found initially by ryokousha, rangsk, and Philip Newman (PN below). An exhaustive search using a gauntlet showed that these are the only four (github, forum). This is the theoretical minimum, as at least this many digits are needed to disambiguate the digit permutation.
- If givens are restricted to the borders of the grid, the fewest possible is 10, found by PN (link). For 9 givens, the lowest solution count is 18, found by PN and ryokousha; this has been verified by rangsk.
- If givens are forbidden from touching, even diagonally, then the fewest possible is 9, found by ryokousha (link). This is the theoretical minimum, as all 8c anti-knight puzzles are known.
- Most anti-knight snipes are known for being terribly unhumanable. The closest anyone has come to a 9-given puzzle that resolves with only singles is TopAutism, with 67 cells filled (link).
Anti-King
- The fewest givens in an anti-king sudoku is 11, found by PN in collaboration with ryokousha (link). It is believed this is minimal, but this has not been proven.
Anti-King + Anti-Knight
- With both anti-king and anti-knight constraints, there is exactly one "essentially different” solution grid (which can be rotated, reflected, or have the digits permuted, to obtain the full list of possible solutions). The fewest possible givens remains 8 in order to disambiguate the digit permutation.
Diagonal (Sudoku X)
- The fewest givens known in a diagonal sudoku is 12; over 500,000 such puzzles are known (link). It is not known whether 11 is possible, though a number of 11c puzzles with 2 solutions are known (including four with 8 distinct digits, found by ryokousha).
Diagonal + Anti-King
- The fewest givens in a sudoku with both diagonal and anti-king constraints is 9, found by PN (link); there are 3 examples known currently. This is believed to be minimal, but this may be proven or disproven by exhaustive search (see above anti-knight section).
Non-Consecutive
- The fewest givens in a non-consecutive sudoku is 4, first determined by Sam Cappleman-Lynes ([2]) who also produced an exhaustive list (link).
- The fewest unique given digits needed for a non-consecutive sudoku is 1, discovered by Freddie Hand (link).
"Miracle" (Non-Consecutive + Anti-Knight + Anti-King)
- The fewest givens with anti-knight, anti-king, and non-consecutive constraints ("Miracle Sudoku") is 2, found by Mitchell Lee (link). This ruleset takes its name from the video linked. It has exactly 72 possible solution grids, which are equivalent to one another up to rotation, reflection, and cycling of digits.
Kropki (Anti-Ratio + Non-Consecutive)
- The fewest givens for a dotless kropki — that is, non-consecutive and anti-ratio (2:1) — is believed to be 4, like non-consecutive on its own. There are 8448 dotless solution grids Template:Citation needed. All of them are roped in both directions, and fully roped (using the same three triples in all boxes) in at least one direction. The fully roped triplets come precisely from the options: 125, 138, 145, 147, 158, 159, 237, 257, 268, 347, 359, 378, 379, or 469.
Kropki (Anti-Ratio + Non-Consecutive) + Irregular
- The fewest givens for an irregular dotless kropki is 0, found by PN (link). Several of these are known, and this category has come to be referred to as a Scooby (after the title of the linked puzzle). We are reasonably confident that you can’t have -1 givens.
Anti-XV
Anti-Ratio + Anti-XV + Irregular
- The fewest givens for an irregular anti-ratio anti-XV grid is 0, found by PN (link).
Disjoint Groups
- The fewest givens in a disjoint groups sudoku is 11 (link). It seems to be minimal, but has not been verified.
Hypercube
- The fewest givens in a hypercube sudoku (disjoint groups + minirows and minicolumns, not to be confused with 3D sudoku) is 8 (link), found by Guenter Stertenbrink. This is the theoretical minimum.
Windoku
- The fewest givens in a windoku is 11 (link), found by Andries Brouwer.
Windoku + Diagonal
- The fewest givens in a sudoku with both windoku and diagonal constraints is 9 (link).
Magic
- The fewest givens in a magic sudoku is 7 (link), found by Guenter Stertenbrink. It is unknown if this is minimal.
2-Quasi-Magic
- The fewest givens in a 2-quasi-magic sudoku is 4 (link), found by Tony Forbes. It is suspected that this is minimal.
Indexing
- In a column-indexing sudoku (or, equivalently, a row-indexing sudoku), the fewest givens required is 7 (link), found by PN. The best known result for 6 givens is 4 solutions (link), also found by PN.
Deconstruction
- In an 11x11 deconstruction sudoku with unspecified regions, the fewest givens required is 12 (link), found by TopAutism. If the regions are given, the fewest is 10 (link), also found by TopAutism.
- If the deconstruction grid is constrained to 10x10 in size, the fewest givens is 14 (link), found by lepton.
Local Constraints
Sukaku
- The highest number of candidates in a pencil-mark sudoku is 643 (86 candidates eliminated), found by tdillon (link link).
Killer
- The fewest cages in a killer sudoku with no givens is 6 (link), and the fewest cells covered is 18 (link), both found by PN. The former is believed to be minimal, but this has not been proven (and 7 was believed to be minimal before the 6 was found, so...). It has since been reduced to cover 26 cells, with no cage larger than 5 in size (link).
- The minimum of 18 cells has been proven by Scott Bathurst and PN (link) by filtering known 17 given classics. The existence of a 17-cell killer would imply the existence of a 17-given classic with the killer cells as givens (this is strictly more information than the killer cages give). Only 1 of the 49158 17-given classics passed the first two filters used - requiring the puzzle to be morphable into a form such that every given is adjacent to at least one other given with the property that switching these two givens results in 0 solutions (if swapping the givens results in 1 or more solutions, then replacing them with a killer cage can never disambiguate between these possibilities) - and this cannot be made unique with only killer cages by inspection. It has since been shown that all 49158 17-given classics are known, completing the proof that there is no 17-cell givenless killer.
- If repeated digits are allowed, 1 cage is sufficient (link); it is unknown who discovered this originally. The minimum sum is 120, and the maximum sum is 285.
- In a traditional killer sudoku (where every cell must be covered), the fewest number of cages is 10 (link), found by TopAutism. This is the theoretical minimum.
- For a latin square, the fewest number of cells covered is 20 (link), found by PN.
- The fewest 2-cell cages is 9 (link) found by PN, again covering the theoretical minimum of 18 cells.
- The smallest number of 2-cell cages with unique totals is 10, as found by PN (link).
- The greatest number of 2-cell cages with unique totals is 14, and it is possible to arrange those cages in a loop in sequential order, as found by PN (link).
- The fewest 2- or 3-cell cages is 7 (link) found by PN, again covering the theoretical minimum of 18 cells.
- The fewest 2-cell cages with all different totals is 10 (link), found by PN.
- The fewest 7-cell cages is 9, as found by SSGranor (link).
- The fewest 8-cell cages is 9, found by Reson (link).
- For 6x6, the fewest is 4 cages and 9 cells, found by spaanse and Vorados (link). This has been proved by spaanse to be both the minimal cell coverage and the minimal number of cages.
- For 6x6, the fewest 4-cell cages is 5, found by PN (link).
- For 6x6, the fewest 5-cell cages is 6, found by PN (link). Four cages is possible with as many as two of them being 5-cell in size (link).
- The fewest digits required in killer cage totals is 5 (5 single-digit totals), found by TopAutism (link). This is the theoretical minimum — although 4 clued cages would be sufficient to disambiguate the digits 1-9, at least one would need a double-digit total.
- The greatest number of cells that can be covered entirely by cages summing to 9 is 77 (link), found by TopAutism. This is not the largest area in general for a single total, as 15 and 45 can both cover the entire grid.
- The fewest number of distinct cage totals needed is 1; this can be done for the following values. All other totals permit digit permutations that guarantee more than one solution.
| Sum | Found by |
|---|---|
| 8*, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 | clover |
| 25 | Joseph Nehme |
| 26 | clover |
| 27 | ahaupt |
| 28, 29, 30, 31 | clover |
| 32 | Joseph Nehme |
| 33, 34, 35 | clover |
| 37 | Sam Cappleman-Lynes |
*requires a 1-cell cage
- For 6x6, the following totals are possible. All other totals permit digit permutations that guarantee more than one solution.
| Sum | Found by |
|---|---|
| 8, 10, 11, 13 | PN |
Killer + Anti-Knight
- The fewest cages is 4, found by ryokousha (link). This is the theoretical minimum, as 3 cages cannot disambiguate 9 digits. The fewest cells covered is 12, found by jovi_al (link), which is also the theoretical minimum.
- For 6x6, the fewest is 3 cages and 7 cells, found by PN (link). This is the theoretical minimum for both, as any lower is insufficient to disambiguate the digits.
- The fewest 2-cell cages is 6 (link) found by ryokousha.
Killer + Anti-King
- For 6x6, the fewest is 3 cages and 7 cells, found by PN (link). This is the theoretical minimum for both, as any lower is insufficient to disambiguate the digits.
Killer + Diagonal
- For 6x6, the fewest is 3 cages and 7 cells, found by PN (link). This is the theoretical minimum for both, as any lower is insufficient to disambiguate the digits.
Killer + Anti-King + Diagonal
- The fewest cages is 5, found by PN (link).
Killer + Non-Consecutive
- The fewest cages is 2. It is not possible to get a unique grid with one cage, but the best possible results for any given cage size are: 389 solutions for a 4-cell cage (link), 11 solutions for a 5-cell cage (link), 20 solutions for a 6-cell cage (link), 11 solutions for a 7-cell cage (link), 69 solutions for an 8-cell cage (link), and 18 solutions for a 9-cell cage (link), all found by Rangsk.
- The fewest 2-cell cages is 3 (link) found by Rangsk. The fewest solutions for a two-domino puzzle is 20 (link), also found by Rangsk.
- The fewest 2- or 3-cell cages is 2 (link) found by Rangsk.
- The fewest 7-cell cages is 9, found by SSGranor (link).
Killer + Anti-Knight + Non-Consecutive
- The fewest cages is 1, and the fewest cells is 3, found by PN (link).
Killer + Cage Inequalities
- The fewest given relations between cages in a killer sudoku is 8, as found by Miyuki Misawa (link).
Thermo
- The fewest thermos is 3, originally found by PN; the fewest cells covered is 20, found by blue (link - note that this is called "17c" in the post, referring to the number of greater-than constraints rather than cells covered; as a result, the thermos in this puzzle are purely orthogonal). It is believed that the former is minimal, as a 2-thermo puzzle would require a corresponding 18c classic, but while these are relatively rare they have not been exhaustively cataloged, nor has a search been made to check for whether any can be morphed to a 2-thermo puzzle. It is unknown whether the cell count is minimal — puzzles with as few as 3 solutions are known for 3 thermos and 19 cells (link).
- For 6x6, the fewest is 2 thermos (link). This is the theoretical minimum.
- If branching thermometers are counted as one, then the fewest is one thermo covering 28 cells, found by PN (link).
- If limited to 2-cell thermos, the fewest is 18 if they are allowed to overlap at bulbs, found by PN and ryokousha collaboratively (link), and 19 if not, with two examples found by ryokousha (link) and PN (link) independently. It is unknown whether these are minimal.
- For 6x6, if limited to 2-cell thermos, the fewest is 8 (link), found by PN. The smallest number of solutions for 7 2-cell thermos is 2 (link, link), also found by PN.
- For 4x4, if limited to 2-cell thermos, the fewest is 3 (link), found by PN.
- The minimum number of non-overlapping 2-cell thermometers required for a puzzle to have no solution is 9. It is suspected that this is minimal.
Thermo + Anti-Knight
- The fewest thermos is 1, and the fewest cells covered is 9, found by PN (link). This is the theoretical minimum for both — at least 8 comparisons are needed to disambiguate the digits.
- If limited to 2-cell thermos, the fewest is 10, found by ryokousha (link). It is unknown whether this is minimal.
- If limited to 3-cell thermos, the fewest is 5, found by ryokousha (link). The lowest known number of solutions for a puzzle with four thermos is 774 (link), also found by ryokousha.
Thermo + Non-Consecutive
- The fewest cells covered by thermometers in a non-consecutive puzzle is 5 (link), found by PN.
- For 6x6, the fewest is 4 (link), found by Lavaloid. This is the theoretical minimum, as 6x6 non-consecutive always allows swapping of columns 1 and 2 and columns 5 and 6. A 3-cell thermo cannot resolve both, so the minimal number of solutions is 2, as shown by Rangsk (link).
- If limited to non-joining 2-cell thermos, the fewest is 8, found by ryokousha (link).
Thermo + 3D
- The fewest thermos in a 3D puzzle is 1, as found by zygoloid (link). The number of cells covered it 9, although it is unknown if this is minimal.
- The fewest inequalities in a 3D puzzle is 7, as found by ryokousha (link). It is unknown if this is minimal.
Slow Thermo
- The longest possible slow thermo is 27 cells, found by PN (link). This is the theoretical maximum.
- The fewest slow thermos is 2 (see previous link). This is the theoretical minimum.
Arrow
- The fewest arrows with single-digit sum is 5, and the fewest cells covered is 21, both found by PN in collaboration with (based on a puzzle by) BlueJay (link). It is unknown whether either is minimal.
- If two-digit sums are allowed then 1 arrow is sufficient, as found by PN, based on the Antiknight Arrow by Gliperal and the single repeats-allowed cage (link). It is unknown if this can be done with the arrow only moving orthogonally.
- For 6x6, the fewest is 3 arrows covering 11 cells, found by PN (link).
- If branching arrows are counted as one, then the fewest is 1 arrow covering 23 cells, found by PN (link).
- If the arrows are restricted to 2-cells, then the minimum is 9 (link), found by PN.
- If the arrows are restricted to 3-cell arrows, each contained within one house, then the minimum is 7 (link) found by PN.
- Certain grids are possible to completely cover with arrows, such that every cell belongs to exactly one arrow.
- Allowing for 2-digit pills or bigger makes it possible to have entirely symmetrical arrow puzzles:
- 90-degree rotational symmetry (link), found by PN
- Horizontal symmetry (link), found by PN
- Diagonal symmetry across the positive diagonal (link), found by KenGlue
- If diagonal arrow pills are allowed to disambiguate symmetry across the negative diagonal, then every symmetry is possible at once, as found by TopAutism (link).
Arrow + Anti-Knight
- The fewest arrows (single digit sums) is 3, found by PN (link). This is the theoretical minimum (with two arrows you can have at most seven distinct digits).
- If two-digit sums are allowed then 1 arrow is sufficient, as found by Gliperal (link).
Arrow + Non-Consecutive
- The fewest arrows is 1, and the fewest cells on that arrow is 5 (link) found by PN. The smallest number of solutions known for a 4-cell arrow is 4 (link), also found by PN.
Arrow + Non-Consecutive + Anti-Ratio
- The fewest arrows in a kropki grid is 1, as found by Gliperal (link).
- If restricted to straight arrows, the fewest is 2, as found by PN (link link).
Kropki (with negative constraint)
- The fewest dots (with negative constraint otherwise) is 1, found by jovi_al (link). This is the theoretical minimum. (Interestingly, this dot can be either white or black.)
Kropki Pairs
- The fewest dots for a kropki pairs sudoku (no negative constraint) is 14, found by PN (link). It is unknown whether this is minimal. At least two white dots are required to disambiguate the digits.
- For 6x6, the fewest dots is 7, found by PN (link). It is unknown whether this is minimal.
- For 4x4, the fewest dots is 4, covering 5 cells, found by Conflux (link).
- For 3x3, the fewest dots is 3, covering 4 cells, found by Conflux (link). This is the theoretical minimum.
- The fewest dots with an equal number of white and black dots and where no dot can be removed and remain unique is 8 of each dot (16 in total), found by PN (link) based on a setup by TopAutism. It is unknown whether this is minimal.
- The longest possible chain of consecutive pairs is 32, which can also be done in a loop, found by MikoKisai (link).
- The longest possible chain of ratio dots is 15, found by armadilloappreciationsocietyzach (link).
Kropki Pairs + 3D + Disjoint Groups
- The fewest dots is 1, found by juggler (link).
Quadruples
- The fewest known number of quadruple clues needed for a unique solution is 7 with 4 digits in each quadruple, found by PN (link). It is believed 7 quadruples is minimal, but this has not been proven; it is also unknown whether 7 quadruples with fewer than 4 digits in at least one quadruple is possible.
- The fewest number of quadruples if each one can only contain a single digit is 28, found by TopAutism (link).
- The fewest total digits in quadruples is currently 27, found by PN (link); it is unknown if this is minimal.
Palindrome
- The longest palindrome possible is 73 cells, found by PN (link). This is the theoretical maximum, since only one digit can appear an odd number of times (the digit at the center of the palindrome).
- The fewest number of cells covered by palindromes required to uniquely color the grid is 26 (link), found by PN. The fewest solutions for a 24-cell coverage puzzle is only 2 (link), found by ryokousha.
Palindrome + Anti-Knight
- The fewest number of cells covered by palindromes required to uniquely color an anti-knight grid is 8 (link), found by PN. This is believed to be minimal.
Palindrome + Anti-King
- The fewest number of cells covered by palindromes required to uniquely color an anti-king grid is 19 (link), found by Gliperal.
Clone
- The largest clone possible is 48 cells, found by TheCoolOne (link).
- The largest clone possible without overlap is 30, found by Botaku (link).
- The maximum number of times a clone domino can appear in a sudoku without overlapping is 8, proven by thirdmunky and Botaku (actually, they provied the more general case of a non-overlapping domino which can take any orientation). If the sudoku is considered toroidally, 9 dominoes are placeable Template:Citation needed.
- The maximum for non-overlapping three-cell clones is also 8, found by Botaku (link).
- The maximum for non-overlapping 3x3 clones is 5 Template:Citation needed. The 3x3 clone in this case must form an extra region (a digit appearing twice in the clone would need to appear 10 times in the grid).
Magic Square
- The maximum number of non-overlapping magic squares is 5 (see above clone section).
X-Sums
- The fewest known number of X-Sum clues needed for a unique solution is 7 (link). This is believed to be minimal, but has not been proven.
- The fewest number of distinct sums needed is 1; this can be done for the following sums:
| Sum | Found by |
|---|---|
| 15 | clover |
| 17 | PN |
| 18, 19, 20 | clover |
| 21 | Astral Sky Ranger |
| 23, 24, 25, 26, 27 | PN |
| 28 | Sam Cappleman-Lynes |
| 30, 31, 32, 33, 35 | PN |
- This list is believed to be complete; it has been proven impossible for sums <= 13 and >= 37 (by marek stefanik), and the sums 16, 22, 29, and 34 only have two values for X, resulting in a maximum of 8 clues (believed to be insufficient for this more restricted problem). The fewest solutions for a puzzle with only 36-sums is 38 (link), which is also believed to be the minimum.
- The largest possible total of all the x-sums on one edge of the grid is 264, as found by zzw (link). This is the theoretical maximum.
Sandwich
- The smallest possible total of all the sandwich sums in a puzzle is 16 (link). This is believed to be minimal.
- The largest total of all the sandwich sums in a puzzle is 363 (link) found by Vorados. It is unknown if this is maximal.
- The smallest possible total of all the sandwich sums for rows is 6 (link) found by PN. This is probably minimal, although I don't remember why.
- The largest possible total of all the sandwich sums for rows is 183 (link). This is the theoretical maximum.
- The fewest distinct sandwich totals possible is 2 (link), found by Reson. This it the theoretical minimum, as demonstrated by brute force. zzw showed that it is possible for the sums to be non-zero, if and only if the two sums total to 35 (link).
- For irregular sudoku it is possible to have a single distinct total, and is possible for precisely the sums 16, 17, or 18, as shown by zzw (link).
- The fewest number of distinct sums needed to resolve a grid up to exchange of 1s and 9s is 1. This can be done with sums of 12, 13, 16, 17, 18, 19, 22, and 23, all found by SSGranor. All other possible sandwich sums have digit permutations that would prevent digits from all being distinguishable.
- The maximum number of sandwiches of a given width has been proven for the following sizes:
| Width | Count | Found by |
|---|---|---|
| 0 | 15 | zzw |
| 1 | 15 | zzw |
| 2 | 12 | zzw |
| 3 | 15 | zzw |
| 4 | 14 | jovial |
| 5 | 11 | jovial |
| 6 | 8 (trivial) | |
| 7 | 4 (trivial) |
(actually I'm not sure 0 has been proven, but it feels correct)
Sandwich + Anti-Knight + Non-Consecutive
- The fewest sandwich clues required is 2 (link), found by Gliperal, which is the theoretical minimum, as 1 clue would allow the grid to be mirrored.
Little Killer
- The fewest known number of Little Killer clues needed for a unique solution is 5 (link), found by Bastien Vial-Jaime.
- The fewest number of distinct sums needed is 1; this can be done for all sums from 12 to 48 and no others:
| Sum | Found by |
|---|---|
| 12 | SSGranor |
| 13, 14, 15 | PN |
| 16 | clover |
| 17, 18, 19, 20, 21, 22, 23 | AFrayedKnot |
| 24 | PN |
| 25 | clover |
| 26, 27, 28, 29, 30, 31 | SSGranor |
| 32, 33, 34 | AFrayedKnot |
| 35 | PN |
| 36, 37, 38 | SSGranor |
| 39 | AFrayedKnot |
| 40, 41, 42, 43, 44, 45, 46, 47, 48 | SSGranor |
- The fewest solutions for a puzzle with only 11-sums is 2 (link), found by ryokousha. This has been proved minimal by zzw. Puzzles exist where all clues are less than or equal to 11 (link) Template:Citation needed.
- A unique solution using one distinct sum is trivially impossible for sums lower than 8. Sums greater than 48 have been proved impossible by SSGranor - on principle for sums above 61 and by exhaustion for the rest - and those from 8-11 have been proved impossible by exhaustion by zzw. The maximum number of digits possible to force for each sum is: 32 for 8 (link), 45 for 9 (link), 41 for 10 (link), and 65 for 11 (link).
- For 6x6, the following totals are possible:
| Sum | Found by |
|---|---|
| 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 | rubenscube |
- The minimum known sum of all little killer clues required for a unique solution is 119 (link), found by rubenscube. The smallest number of solutions for a total sum of 117 is 2 (link), found by TopAutism. It is unknown if either is minimal.
Little Killer + Non-Consecutive
- The fewest number of little killer clues in a non-consecutive puzzle is 2, found by PN (link).
Skyscrapers
- The fewest number of distinct Skyscraper clues needed is 1; this can be done for the following values:
- 5 - link (found by PN)
- 6 - link (found by SSGranor)
- The fewest solutions for a puzzle with only 4-clues is 4 (link) found by Youri.
- The fewest solutions for a puzzle with only 3-clues is 8 (link) found by AFrayedKnot.
- The fewest solutions for a puzzle with only 2-clues is 2, all of which rely on using 8 clues on one edge. It can be proven that this is insufficient for a unique solution, however, and the prospects of any other arrangement seem very bleak.
- For diagonal skyscrapers, the fewest number of clues required is 4 (link), found by PN.
German Whispers
- German whispers cannot result in a unique solution on its own, due to the symmetry of the digits; any solution can be transformed to a different valid solution by mapping each digit X to 10-X.
- The minimum number of cells covered by a single line resulting in only two solutions is 19 found by PN (link). This is a total of 18 connections/comparisons between cells, also the minimum known. The best known for 18 cells/17 connections has 36 solutions. It is unknown if allowing branching can improve on this.
- The longest single line possible covers 60 cells, found by Reson (link). It is unknown if this is maximal.
First and Last Impressions?
- The maximum number of clues is 31 (link), found by Sam Cappleman-Lynes.
Pro-King
- The maximum number of pro-king cells is 52 (link), found by PN.
Activated Cells
- The fewest possible activated cells in a sudoku grid is 11, first found by SSGranor (link). This is the theoretical minimum, as every row will have at least one, and rows with 5 on the edge will have two.
- The most possible activated cells in a sudoku grid is 36, first found by Youri (link). It is also possible for the activated cells to form a single orthogonally connected region, as shown by Reson (link). It is unknown whether a snake is possible.
Renban
- Like German Whispers, Renban cannot result in a unique solution on its own, due to the symmetry of the digits; any solution can be transformed to a different valid solution by mapping each digit X to 10-X.
- The minimum number of renban lines required to reduce a grid to two solutions is 8 (link), found by TopAutism. It is unknown if this is minimal.
Full Rank
- The fewest full rank clues is 6 (link), found by sigh. It is unknown if this is minimal.
X-V
- The maximum number of X-V clues is 60, as discovered by PN (link). It is unknown if this is maximal.
X-V + Anti-XV
- The fewest X-V clues (with negative constraint) required to reduce the grid to 8 solutions (the minimum possible without givens) is 5, found by PN (link).
Region Sum Lines
- The fewest number of region sum lines required is 1 (link), found by AFrayedKnot. This is also possible if the line is required to form a loop (link, TopAutism) or travel orthogonally (link, PN).
- For 6x6, the fewest is also 1 (link), found by PN, and can also be done in a loop (link, TopAutism).
Fog of War
- The fewest number of initially lit givens required for a fog of war sudoku is 4 (link), found by TopAutism. This is the theoretical minimum, but it is unknown if the number of total givens for such a puzzle (currently 20) can go lower.
- With traditional illumination rules (cells initially illuminated by bulbs that cover a 3x3 area), the best known is 5 givens (link), found by PN.
Odd / Even
- Allowing an unlimited number of odd/even clues, the minimum number of givens required is 7, essentially discovered by dobrichev and coloin (link) and put into a puzzle by marek stefanik (link). This is the theoretical minimum.
Size / Entropy
- The fewest number of size/entropy clues is 21, found by TopAutism (link).
Arrows where the digit on an arrow is greater than all digits in the indicated direction
- The fewest number of arrows is 9, found by PN (link). The fewest known solutions for 8 arrows is 16, also found by PN.
Self-Counting Circles
- The maximum number of self-counting circles is 45, found by zzw (link).
Convex Hull
- The maximum number of digits in a sudoku grid with an 8-vertex convex hull is 6, found by zzw and PN (link).
- It is possible to have a unique grid by only specifying the convex hulls of each digit, as found by zzw (link).
10-Lines
- 10-lines are lines which must be divided into non-overlapping segments which each sum to 10.
- Only one 10-line is necessary to make a puzzle unique, found by AFrayedKnot (image: link, f-puzzles: link).
Zipper Lines
- Digits equidistant from a zipper line's center must sum to the same value. If odd length, the center cell must equal that sum.
- The minimum number of zipper lines to force a unique solution is two, found by AFrayedKnot (image: link, f-puzzles: link).
Miscellaneous
Grid Properties
- There exist solved 9x9 latin squares which cannot be divided into sudoku regions aside from the trivial row and column partitions. The first known was found by PN and proven by AFrayedKnot (link).
- There exist solved sudoku grids which exhibit all three types of symmetry: rotational, reflectional (on both diagonals), and translational. The first recorded example comes from shye (link).
- There exist pencil-mark sudoku that have exactly two solutions which share no digits in common, first documented by jovi_al (link).
- It is possible for one digit in a sudoku grid to completely avoid touching (even diagonally) two others, as discovered by Emphyrio (link). The properties hold toroidally as well. Up to isomorphisms, it is the only pattern that works.
- For a symmetric, non-consecutive grid, the minimum amount of roping is two bands and one stack, found by shye (link). It is unknown if better is possible.
- There exist sudoku solutions that can be divided into two sets of digits, such that any orthogonally connected group in either set contains no repeated digits, as demonstrated by JMoat13(link) using a 4-digit/5-digit split. It is believe to be impossible for a 3-digit/6-digit split, even if the restriction on the 3-digit clusters is lifted.
- The minimum number of distinct sums of orthogonally adjacent digits in a filled sudoku grid is 7 (link) found by PN, this is the minimum, proven using a SAT solver by nathanf. Manually, a lower bound of 6 has been proven by rubenscube Template:Citation needed.
- The minimum number of regions into which a solved grid can be partitioned, such that any one region can be deleted without adding solutions, is 3. Youri was first to describe the trivial partition where each region consists of 3 boxes, one from each band and stack. If the regions are required to be orthogonally connected, then the best known is 5 (link) found by AFrayedKnot. For specific grids, this can be improved to 2 (link), also found by Youri.
- There also exist specific grids which can be partitioned into 3 or even 4 sets of digits, such that each group individually (that is, deleting all other groups) still results in a unique solution. The first of these "Troikas" were found by Mathimagics (link); in fact, the linked grids are "Perfect Troikas" in that they are partitioned into equal (27-cell) sets and each resulting grid is minimal. The first "Quadriga" was found by coloin (link).
- Every solution to a sudoku grid contains some set of 21 cells (or less), which make a uniquely solvable puzzle. 21 has been proven to be the minimum in this regard by Mathimagics, using exhaustive search (link). The search also proved that there are only 4 essentially different grids which contain 21C puzzles, but no 20C puzzles, which were first discovered by blue in this thread.
- The maximum number of extra regions that can exist in a classic sudoku grid is 24. It is suspected that this is maximal, and requires a fully-roped grid.
- There exists a numbered rooms grid with one set of the clues 1-9 on each edge of the grid, found by nathanf (link), with a unique solution.
- The smallest possible sum of the clues in a numbered rooms puzzle is 40, found by jmerry (link). In an even-sized grid it is possible for all of the clues to be 1, as shown on 16x16 by PN (link).
- The maximum number of impossible orthogonal pairs that can exist in a sudoku grid is 18.
- The maximum number of deadly patterns in a variant sudoku is 16, found by TopAutism (link).
- The maximum number of deadly patterns in a classic sudoku is 11, found by TopAutism (link). Interestingly, the grid also doubles as a 16-solution for variant sudoku.
- The maximum number of anti-queen digits (that is, digits which never appear more than once on any diagonal) is 7.
- The maximum number of digits in a bishop team (that is, digits which never appear on a diagonal with a different digit from the same team) is 3, as found by nathanf (link). This grid has the additional property that it has three teams of bishops.
- The maximum number of friendly cells possible in a sudoku is 27, one each for the nine rows, columns, and boxes. It is possible to make a snake that contains all such digits, as found by PN (link).
- There exist solved sudoku grids for which every diagonal sums to a distinct total, as shown by Sam Cappleman-Lynes (link).
- Non-consecutive grids exist with no repeated triples, as shown by Rangsk (link).
- There exist grids that contain a 44-cell-long snake that does not touch itself orthogonally and consists only of odd digits. There are no grids that contain a 45-snake if it starts in a corner (nathanf).
- There exist grids that contain a 36-cell-long loop that contain all the even digits, if allowed to travel diagonally, as found by PN (link).
- The maximum number of 9-digit square numbers that can be fit into a sudoku grid is 5, found by Manus Hand (link).
- There exist solved sudoku grids that are both diagonally non-consecutive and diagonally non-equal (anti-king), as shown by ryokousha (link).
- There exist latin squares that are both orthogonally and diagonally nonconsecutive, as shown by nmay231 (link).
- There exist solved sudoku grids in which every digit is orthogonally adjacent to every other digit at least once, as shown by Sonic (link).
- There exist solved sudoku grids in which every instance of a 1 is orthogonally adjacent to a 2, as shown by Ben (link). It is also possible for this relationship to be mutual (link).
- There exist solved sudoku grids in which all cells have at least one orthogonally adjacent cell with a consecutive digit, known as Touchy Sudoku, and with examples dating as early as 2007.
- There exist solved 6x6 sudoku grids in which all cells are connected to each other by following orthogonally adjacent consecutive digits (kendfrey).
- There exist latin squares in which all digits are a knight's move away from at least one identical digit (pro-knight), as shown by Alice (link).
- The maximum number of naked singles that are possible at any given time is 12, as found by TheCoolOne (link). Surely this can be improved.
- Cube Nets
- It is possible to fit all 11 unique cube nets in a 9x9 grid, as shown by PN (link).
- If the nets are required to contain the digits 1-6 only, then it is possible to fit 9Template:Citation needed.
- If the nets are required to contain one set of the digits 1-6 each, then it is possible to fit 8Template:Citation needed.
- If the nets are required to fold into valid dice (opposite digits summing to 7), then it is possible to fit 5, as shown by Gliperal (link).
Augmented Classics
- Although it is not possible for a sudoku puzzle to be unique with only given digits along the borderTemplate:Citation needed, many individual constraints are enough to finish the job, including:
Famous Number Classics
- There is a trend of setting classics whose string representation contain as many of the digits of certain famous numbers as possible, in order. In this case zeros are allowed as wildcards, since any character that is not a digit 1-9 is typically treated as an empty cell. Puzzles with unique solutions exist for the following numbers:
Greatest Distance between Givens
- Greatest Euclidean distance around a single given is √40 (link), found by kendefrey.
- Greatest taxicab distance between the closest pair of givens in an irregular sudoku is 4 (link), found by shye.
- Greatest taxicab distance between the closest pair of givens in anti-knight is 4 (link), found by shye. This is suspected to be maximal.
- Greatest taxicab distance around a single given in anti-knight is 12 (link), found by Gliperal. This is maximal.
- Greatest taxicab distance between the closest pair of givens in a dotless kropki sudoku is 8 (link), found by shye. This is also the greatest known Euclidean distance, at √50. Both are maximal Template:Citation needed.