Difference between revisions of "Uniqueness"
| (8 intermediate revisions by the same user not shown) | |||
| Line 34: | Line 34: | ||
Uniqueness Techniques (UT) depend on the assumption that a puzzle has a single valid solution '''''at the time of application'''''. This premise often does not hold for incomplete puzzles during the incremental process of setting a puzzle. In such cases, applying UT leads to incorrect, or at best useless deductions, even if subsequent clue additions ultimately render the puzzle unique. | Uniqueness Techniques (UT) depend on the assumption that a puzzle has a single valid solution '''''at the time of application'''''. This premise often does not hold for incomplete puzzles during the incremental process of setting a puzzle. In such cases, applying UT leads to incorrect, or at best useless deductions, even if subsequent clue additions ultimately render the puzzle unique. | ||
Assuming we have determined whether a partial puzzle has a single or multiple solutions by accurately applying non-uniqueness techniques and/or using a computer solver to enumerate the solutions, the following non-mutually exclusive situations may occur: | Assuming we have determined whether a partial puzzle currently has a single or multiple solutions by accurately applying non-uniqueness techniques and/or using a computer solver to enumerate the solutions, the following non-mutually exclusive situations may occur: | ||
=== The current puzzle has more than one solution === | === The current puzzle has more than one solution === | ||
| Line 50: | Line 50: | ||
; Applying a UT leads to zero solutions | ; Applying a UT leads to zero solutions | ||
: Similar to the previous case, this contradiction confirms the puzzle is not unique.<br />We establish the implication <code>unique => no solutions</code>, but the consequence is not necessarily true since the premise is false. | : Similar to the previous case, this contradiction confirms the puzzle is not unique.<br />We establish the implication <code>unique => no solutions</code>, but the consequence is not necessarily true since the premise is false.<br />The contrapositive <code>one or more solutions exist => not unique</code> has a true premise, but yields information we already possessed. | ||
The contrapositive <code>one or more solutions exist => not unique</code> has a true premise, but yields information we already possessed. | |||
; Applying Different UTs Leading to Different Solutions | ; Applying Different UTs Leading to Different Solutions | ||
: There may be situations where multiple different uniqueness techniques can be applied to a non-unique puzzle, | : There may be situations where multiple different uniqueness techniques can seemingly be applied to a non-unique puzzle, but result in different solutions depending on which UT is used. It's also possible that applying multiple UTs simultaneously may lead to the conclusion that there are zero solutions. This further demonstrates the potential pitfalls of using UT during the puzzle-setting process, as it can introduce inconsistencies and inaccuracies. | ||
: [[File:Classic_Sudoku_17.png|300px|right|link=MediaWiki|frameless|Contradictory uniqueness deductions]] | : [[File:Classic_Sudoku_17.png|300px|right|link=MediaWiki|frameless|Contradictory uniqueness deductions]] | ||
| Line 62: | Line 61: | ||
::- This grid does, in fact, have three valid solutions. | ::- This grid does, in fact, have three valid solutions. | ||
::- However, using the [[Unique Rectangle|unique rectangle]] in green results in the conclusion 3r7c2, resolving the red rectangle, leading to one specific solution. | ::- However, using the [[Unique Rectangle|unique rectangle]] in green to eliminate 12 from r7c2 results in the conclusion 3r7c2, resolving the red rectangle, leading to one specific solution. | ||
::- Using the [[Unique Rectangle|unique rectangle]] in red instead results in the conclusion 1r7c2, resolving the green rectangle, thereby leading to a different solution. | ::- Using the [[Unique Rectangle|unique rectangle]] in red to eliminate 23 from r7c2 instead results in the conclusion 1r7c2, resolving the green rectangle, thereby leading to a different solution. | ||
::- Using | ::- Using the [[Unique Rectangle|unique rectangle]] in green to eliminate 1 and the [[Unique Rectangle|unique rectangle]] in red to eliminate 3 from r7c2 results in the conclusion 2r7c2, giving a third solution. Alternatively, [[BUG]]+1 can be applied to reach the same conclusion. | ||
::- | ::- Using both [[Unique Rectangle|unique rectangles]] to eliminate the candidates 123 from r7c2 results in no solutions. | ||
=== The current puzzle has exactly one solution === | === The current puzzle has exactly one solution === | ||
| Line 80: | Line 79: | ||
== Speed Solving and Competitions == | == Speed Solving and Competitions == | ||
In speed solving | In speed solving sudoku competitions, the use of UT is common. These events often feature thoroughly tested puzzles designed to have unique solutions, making the uniqueness assumption more justified. Additionally, the competitive nature of these events encourages solvers to use all available techniques, including UT, to achieve the fastest solving times. | ||
== Computer-Generated Sudoku Puzzles == | |||
Computer-generated sudoku puzzles are common, especially for daily online puzzles and large puzzle packs. These puzzles are typically generated using computer algorithms and validated using computer solvers to ensure they adhere to a well-defined set of criteria, most importantly that they have a unique solution. | |||
The rating system of computer-generated sudoku puzzles might include Uniqueness Techniques (UT). In these cases, using these techniques could be considered advisable for solvers to experience the puzzle at the intended difficulty level. Refraining from using UT might unintentionally escalate the puzzle's complexity, making it seem more difficult than it was designed to be. | |||
== Summary == | == Summary == | ||
As a single-player game, sudoku allows solvers to employ any technique they prefer. However, it is essential to understand the logical assumptions underpinning UT to ensure their correct application in specific situations. | As a single-player game, sudoku allows solvers to employ any technique they prefer. However, it is essential to understand the logical assumptions underpinning [[Solving Techniques#Uniqueness Techniques|Uniqueness Techniques]] (UT) to ensure their correct application in specific situations. | ||
Additionally, the appropriateness of using UT may vary depending on the social context and community. For instance, a puzzle setter may not desire solvers to bypass particularly elegant parts of a solution by applying UT. | Additionally, the appropriateness of using UT may vary depending on the social context and community. For instance, a puzzle setter may not desire solvers to bypass particularly elegant parts of a solution by applying UT. | ||
Latest revision as of 12:16, 3 August 2023
This wiki page discusses the use of uniqueness in sudoku, including the debate surrounding whether uniqueness can and should be assumed when solving and when setting sudoku puzzles.
Uniqueness in Sudoku
Uniqueness in sudoku refers to the concept that a well-formed sudoku puzzle should have only one valid solution. This idea is central to various solving techniques known as Uniqueness Techniques which rely on the assumption that the puzzle has a unique solution.
Uniqueness Techniques
Uniqueness Techniques (UT below) are strategies that exploit the unique solution assumption to make deductions while solving sudoku puzzles. These methods identify configurations that would lead to multiple solutions, thereby contradicting the unique solution assumption. By eliminating these configurations (see also Guardians), solvers can make progress towards the correct solution.
Effectiveness of Uniqueness Techniques
Assuming a puzzle has a unique solution, this solution can always be obtained through Trial and Error steps or equivalent reformulations, such as complex nested chains or other specialized solving techniques. Consequently, the use of Uniqueness Techniques (UT) is never strictly required to solve any sudoku puzzle.
The effectiveness of UT spans a wide spectrum: from cases where UT can be applied but may not offer a significant advantage over traditional solving techniques, to situations where using UT considerably simplifies the puzzle or even transforms an otherwise seemingly unsolvable puzzle into one that can be solved by humans. Template:Citation needed
Uniqueness in Puzzle Solving
The use of UT for solving sudoku is not universally accepted, as it hinges on the assumption that a puzzle has a unique solution. While rare, this assumption may not hold true for all sudoku puzzles, particularly those not designed with a unique solution in mind (for example puzzles with relaxed rules such as Schrödinger Cells or similar concepts; see also Fractional Dimension).
Solving a sudoku puzzle without using UT offers a stronger validation of the puzzle's well-formedness. When a solver completes a puzzle without relying on UT, they inherently prove that the puzzle has a unique solution. Conversely, using UT may lead to a solution that is only one of many, without providing information on whether the solution is, in fact, unique.
This distinction is particularly important in test solving and providing feedback to the puzzle setter. Solving a puzzle without using UT allows the solver to confirm that the puzzle is indeed well-formed, an essential quality check for the setter.
Puzzle setters intending the use of UT are encouraged to include clear language in the puzzle rules, explicitly stating that the puzzle has a unique solution, thereby legitimizing and hinting at the use of UT for the solvers. Puzzle rules can include phrasings such as: "This puzzle has a unique solution." or more explicitly, "This puzzle has a unique, computer-verified solution. Feel free to use this fact during your solving process."
In the absence of such wording, it is not always safe to assume that the setter intended the use of UT. Therefore, by avoiding UT and relying solely on logical deductions within the puzzle's constraints, solvers not only ensure that the puzzle has a unique solution but also maintain the integrity of the solving process by avoiding shortcuts not intended by the puzzle setter.
However, in some communities or forums where the assumption of uniqueness is commonly agreed upon, solvers might feel more comfortable using UT even without explicit instructions.
Uniqueness in Puzzle Setting
Uniqueness Techniques (UT) depend on the assumption that a puzzle has a single valid solution at the time of application. This premise often does not hold for incomplete puzzles during the incremental process of setting a puzzle. In such cases, applying UT leads to incorrect, or at best useless deductions, even if subsequent clue additions ultimately render the puzzle unique.
Assuming we have determined whether a partial puzzle currently has a single or multiple solutions by accurately applying non-uniqueness techniques and/or using a computer solver to enumerate the solutions, the following non-mutually exclusive situations may occur:
The current puzzle has more than one solution
- Applying a UT leads to one solution
- This situation establishes the tautology
unique => unique- we have assumed and deduced puzzle uniqueness. While logically true, it doesn't allow for drawing conclusions about the assumption's validity by itself. It is equivalent to its contrapositivenot unique => not uniquethe premise of which is true, but it doesn't provide a meaningful deduction.
- To emphasize the point: We cannot deduce the puzzle being unique despite a previous computer result of it being non-unique in this case. So, we are not "outsmarting" the computer. Instead, we have simply uncovered an "empty" or trivially true statement.
- Applying a UT leads to more than one solution
- This situation presents the contradiction
unique => not unique, as we've assumed uniqueness and deduced non-uniqueness. It results in concluding that the puzzle is not unique, which we already knew.
- Applying a UT leads to zero solutions
- Similar to the previous case, this contradiction confirms the puzzle is not unique.
We establish the implicationunique => no solutions, but the consequence is not necessarily true since the premise is false.
The contrapositiveone or more solutions exist => not uniquehas a true premise, but yields information we already possessed.
- Applying Different UTs Leading to Different Solutions
- There may be situations where multiple different uniqueness techniques can seemingly be applied to a non-unique puzzle, but result in different solutions depending on which UT is used. It's also possible that applying multiple UTs simultaneously may lead to the conclusion that there are zero solutions. This further demonstrates the potential pitfalls of using UT during the puzzle-setting process, as it can introduce inconsistencies and inaccuracies.
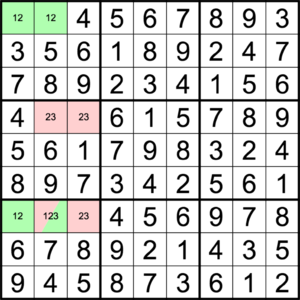
- Consider the following example by Sam Cappleman-Lynes:
- - This grid does, in fact, have three valid solutions.
- - However, using the unique rectangle in green to eliminate 12 from r7c2 results in the conclusion 3r7c2, resolving the red rectangle, leading to one specific solution.
- - Using the unique rectangle in red to eliminate 23 from r7c2 instead results in the conclusion 1r7c2, resolving the green rectangle, thereby leading to a different solution.
- - Using the unique rectangle in green to eliminate 1 and the unique rectangle in red to eliminate 3 from r7c2 results in the conclusion 2r7c2, giving a third solution. Alternatively, BUG+1 can be applied to reach the same conclusion.
- - Using both unique rectangles to eliminate the candidates 123 from r7c2 results in no solutions.
The current puzzle has exactly one solution
- Applying a UT leads to one solution
- This is the only situation permitting a meaningful deduction since the UT's premise is true. While we don't acquire new information about the number of solutions (as we already know the puzzle is unique), the eliminations resulting from applying the UT are valid.
This knowledge can help puzzle setters assess the UT's impact on the solving process, allowing them to either accept the deductions for the intended solving path or modify the puzzle to avoid such deductions.
- To be perfectly clear: The knowledge that the current puzzle has exactly one solution must come from an external source, either traditional non-uniqueness techniques or a computer solver, for these deductions to be valid.
Speed Solving and Competitions
In speed solving sudoku competitions, the use of UT is common. These events often feature thoroughly tested puzzles designed to have unique solutions, making the uniqueness assumption more justified. Additionally, the competitive nature of these events encourages solvers to use all available techniques, including UT, to achieve the fastest solving times.
Computer-Generated Sudoku Puzzles
Computer-generated sudoku puzzles are common, especially for daily online puzzles and large puzzle packs. These puzzles are typically generated using computer algorithms and validated using computer solvers to ensure they adhere to a well-defined set of criteria, most importantly that they have a unique solution.
The rating system of computer-generated sudoku puzzles might include Uniqueness Techniques (UT). In these cases, using these techniques could be considered advisable for solvers to experience the puzzle at the intended difficulty level. Refraining from using UT might unintentionally escalate the puzzle's complexity, making it seem more difficult than it was designed to be.
Summary
As a single-player game, sudoku allows solvers to employ any technique they prefer. However, it is essential to understand the logical assumptions underpinning Uniqueness Techniques (UT) to ensure their correct application in specific situations.
Additionally, the appropriateness of using UT may vary depending on the social context and community. For instance, a puzzle setter may not desire solvers to bypass particularly elegant parts of a solution by applying UT.
Employing UT while creating puzzles is, for almost all cases, inadvisable.
Pros
- UT can simplify and speed up the solving process, allowing solvers to eliminate possibilities more efficiently.
- In many cases, sudoku puzzles are designed with the intention of having a unique solution, making the use of UT valid and appropriate.
- Exploiting uniqueness can provide interesting and satisfying logical deductions for the solver.
- In some communities, uniqueness might be a shared implicit assumption and not using UT can result in unintentionally difficult solves.
Cons
- Solving a puzzle without using UT proves a stronger result (the existence of a single solution rather than the existence of a solution), which solvers may find more satisfying.
- Relying on UT may lead to incorrect deductions for puzzles without unique solutions.
- Using UT may shortcut the intended solving path, possibly resulting in a quicker but less satisfying solve.
- Some solvers argue that using UT detracts from the pure logic aspect of sudoku, as these methods depend on a meta-assumption about the puzzle rather than working strictly within the puzzle's constraints.
- Puzzle setters may be inclined to use uniqueness while creating the puzzle, leading to incorrect deductions in the majority of situations.